Rational vs. non-rational geometry

Non-rational geometry is a sum of polynomials. Rational geometry is a ratio of sums of polynomials. Rational geometry is considerably more complex mathematically. Therefore:

It may not be transferable to downstream CAD packages that can’t deal with complex descriptions
It can be slower to manipulate when modeling, and slower to render.

The following tables lists the differences between the two types of geometry.

Nature	Pros	Cons
Non-rational	More flexibility for transformations.Faster.	Sacrifices some precision for modeling flexibility.
Rational	Precise geometry (that is, exact conics).	Weighted CVs not supported by many CAD packages. Weighted CVs harder to manipulate.Creates multi-knots.Slower to display and render.

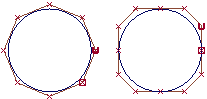
This illustration shows two circles drawn with the two types of geometry.

The circle on the left is a non-rational curve with CVs that are all weighted equally. To have a non-rational curve, all weights must be 1.0.
The circle on the right is a rational curve with different weights applied to the CVs, and multi-knots.

You can see the difference in two ways:

If you attach a radius measurement to the circles, the non-rational circle is not a perfect circle (although it is close): it has different radii depending on where you measure. The rational circle is a perfect circle.
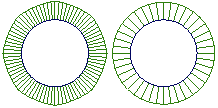
Attach curve curvature combs to the circles. The curvature on the non-rational circle on the left varies. The curvature of the rational circle on the right is constant.