Inverse kinematics is a technique for generating the joint angles for a hierarchy in a way that fulfills geometrical constraints. A constraint is something which reduces the freedom of movement of an object. For instance, a cylinder in a cylinder block is constrained to one degree of freedom, that is sliding along its length.
If a piston rod is to pivot both on a wheel and a cylinder, and the cylinder is to be constrained linearly, then the system only has one degree of freedom. The rotation angle
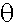
at A determines the angle at B which in turn determines the position of C.
A simple two-dimensional hierarchy has two degrees of freedom. It is the constraint of the cylinder which makes the angle at B dependent on
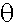
and reduces the degrees of freedom to 1. Computing such dependencies is the focus of inverse kinematics. This requires inverse trigonometric functions and Pythagoras' Theorem.
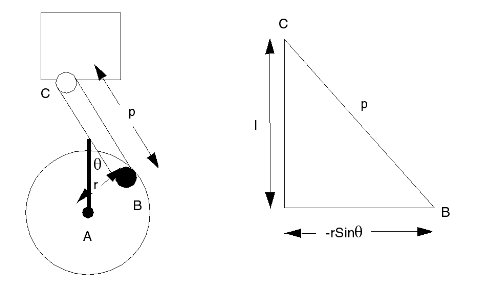
Piston,
Rod and Wheel l2 = p2 - (rSin 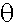 )2
)2
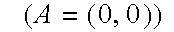
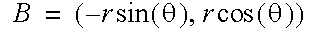
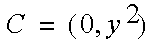
where
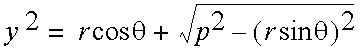
(Pythagoras' Theorem)
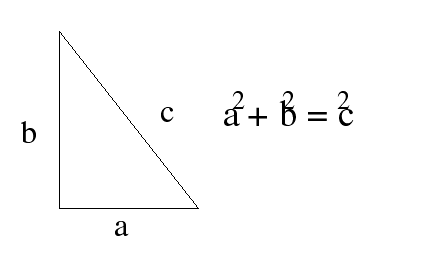
Robot arms are hierarchical devices for gripping and moving objects. The position of the hand or "end effector" is controlled using the joint angles at the shoulder and elbow. Consider a two-dimensional robot:
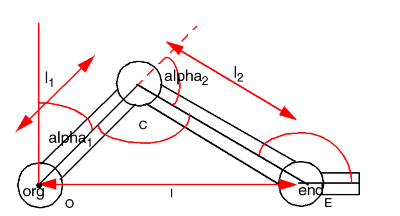
A Two-dimensional Robot
A two-dimensional robot arm is illustrated above. It has two degrees of freedom. The variable alpha1 is the shoulder angle, while alpha2 is the elbow angle. If both are equal to zero the arm points straight up in the air. The end coordinate can be computed from the x1, alpha2 angles and the lengths l1, l2.
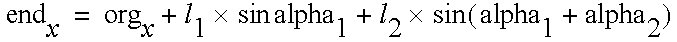
1
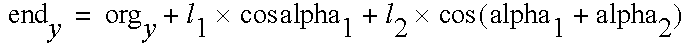
2
This is forward kinematics and can either be used directly in SDL or the hierarchy with joint angles alpha1, alpha2 will do it implicitly. Unfortunately with robots it is usually required to specify the end and origin points explicitly and derive the joint angles from them. This requires inverting equations 1 and 2. Rather than do this directly, it is easier to do this a piece at a time.
Consider the triangle OCE
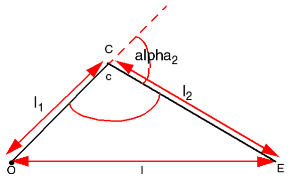
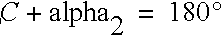
By Pythagoras
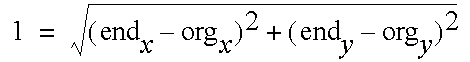
By the Cosine rule
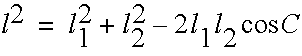
Hence C, hence alpha2.
Computing alpha2 is more difficult
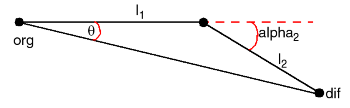
Take
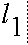
to be horizontal and
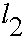
to be at angle
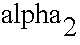
.
The new end point is given by
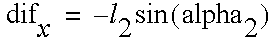
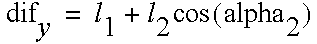
The function atan2 can be used to get
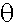
.
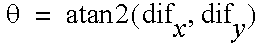
This returns dif to y = 0.
The elevation above the horizontal can be obtained using
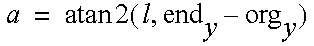
Therefore, alpha1 is given by
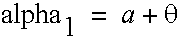
A model can be made a little more complicated by the fact that the end points have a z coordinate as well. However, a three-dimensional case can be reduced to a two-dimensional case by constraining the arm to only lie in a vertical plane.
First, the arm is rotated about the y axis by
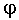
(phi) where
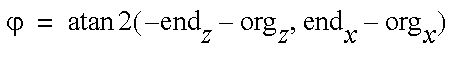
then the two-dimensional equations are solved as before.
The arm so far described stops at the wrist. A real robot has a gripper which can rotate on a ball joint about the wrist.
This may be achieved again using atan2 functions. The robot arm in this example has a target point called (xtarget, ytarget, ztarget). The wrist is positioned at a point defined by the approach vector (xtarget + xapproach, ytarget + yapproach, ztarget + zapproach). The "gripper", which in fact is just a cylinder, always points towards the target.
Try moving the target point outside the reach of the robot. What happens? Try changing the lengths of the segments.