Projectiles are objects which have an initial velocity and then move in a way which depends on the forces acting on them.
The total force f acting on a mass m creates an acceleration a according to the following equation:
f = ma
In a time step,
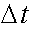
, the new velocity
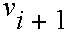
can be derived from the old velocity
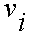
using:
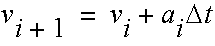
where
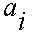
is the instantaneous acceleration. The new position is given by:
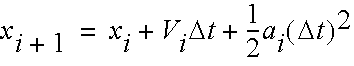
These formulae assume that
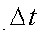
is very small.
Projectiles have an initial velocity
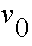
and an initial position
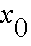
. The force acting on the particle is computed taking into account gravity and atmospheric drag, and the motion path for the projectile results. The equations above work for each coordinate independently.
For a terrestrial cannon ball the effects of gravity are uniform. The force of gravity acts down along the y axis and is proportional to the mass.
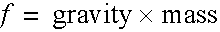
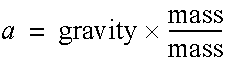
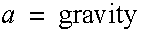
This is Galileo's famous discovery that, in the absence of an atmosphere, all objects fall with the same acceleration. (A cannon ball and a feather hit the ground at the same time if released from the same height on the moon!).
The SDL file CourseWare/SDL/proj simulates a projectile moving through a vacuum. The initial velocities along x and y are computed from a total velocity and an angle of elevation. Try changing the angle to see which angle gives the maximum range for the projectile. Range is defined as the distance it moves through before returning to its initial y value.
Real projectiles, however, move through air. This slows them along their path by creating a frictional force which acts in the opposite direction to the velocity of the projectile (relative to the wind).
Therefore,
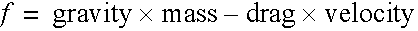
The SDL file CourseWare/SDL/dproj simulates this effect. Try different values of “drag.” Is the optimal elevation angle still 45°?
The effect of the atmospheric drag is to reduce the horizontal velocity eventually to zero, and to slow the ball both in its rise and descent. The ball ultimately ends up descending vertically at a "terminal" velocity. The force of gravity is then equal to the atmospheric drag.
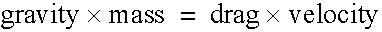
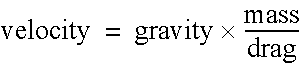
(This is why parachutes are a good idea. The drag is greatly increased so that terminal velocity decreases to the point that parachutists can land safely).
Most cannons, of course, do not float in free space, but sit on the ground. Cannon balls, in the same way, collide with obstacles and bounce. A simple floor may be implemented as follows.
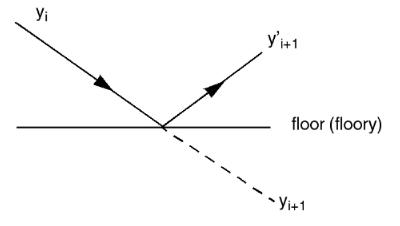
The velocity normal to the surface after the collision is reversed in sign and multiplied by the reflection coefficient called nelasticity. The actual new position is given by:
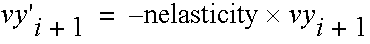
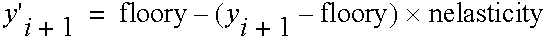
The tangential new velocity is given by:
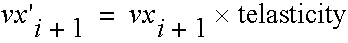
The intersection x coordinate is given by:
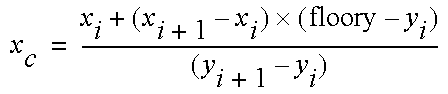
The next x coordinate for the particle is:
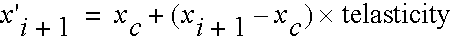
This model is implemented in the SDL file CourseWare/SDL/cproj. Try changing the different values of the elasticities.
While individual projectiles are useful in some circumstances, the true power of procedural animation is revealed when a large number of objects are involved. Consider a roman candle with a spray of sparks issuing from it. Each particle will follow a trajectory that depends on its initial velocity and position. The current velocity and position of each particle have to be stored in SDL variables. This is made easy by defining arrays with an index that refers to the particle number.
The SDL file CourseWare/SDL/roman illustrates how to create a firework of exactly this sort. A looping "for" structure is used to process each particle in turn. The variable "numpart" controls the number of particles in the animation sequence; 10000 is plenty but they take a long time to animate and will not play back in real time using preview. A "numpart" of 300 should prove adequate for motion tests. The individual particles are modeled as cylinders which extend from the previous position to the current one. The rendering is additive, that is, the cylinders are completely transparent with a colored incandescence value. It happens that when large numbers of such particles are rendered on top of each other, the color clips to white. This works rather nicely for the firework.
Unfortunately, the "wireframe" rendering mode uses the color value for the particles. The color value of these particles is actually black. This will lead to black particles on a black background. For wireframe tests, it is necessary to make the color white.
The wind velocity is a global control over the animation. Every particle is affected along its trajectory. The SDL file CourseWare/SDL/roman uses an animate statement to control the wind as a function of time. The wind blows to the right strongly early in the animation and then gusts less later on. Try experimenting with the drag coefficient, the particle velocities and the amount of gravity. Try moving the spark origin point as a function of the birth time to simulate a rocket.
A snow storm may be thought of as a collection of particles. They are created in a condensation or cloud layer. The flakes will have randomly distributed positions and will then fall under gravity. Some flakes will have different drag coefficients and so will fall at different rates. They will also tumble randomly as they fall.
This model is implemented in the SDL file CourseWare/SDL/snow. When rendered, the snow flakes, which are faces, are transparency mapped with images which were derived from photographs of real snow flakes. The wind direction is chosen to be perpendicular to the direction of view. This prevented any snow flakes from blowing too close to the camera and so looking enormous. A useful trick was also employed to prevent the system from running out of snow flakes. The viewing frustum was considered to be looking through an active volume of snow fall. The left and right sides of the volume were outside of the field of view. This volume was defined by ± xrang and ± zrang. Any snow flakes which passed out of the positive x wall were moved to the corresponding spot on the negative x wall. In this way the number of snow flakes was used to best effect.